Crystallography: The Triclinic System
Last Updated: 7th Feb 2021By Donald Peck & Alfred Ostrander
According to the International Union for Crystallography
In some respects, the Triclinic Crystal System is the simplest of the seven systems. In other ways it is the most difficult to comprehend. There is little or no symmetry. And there are only two simple crystallographic forms to consider. Putting these two seemingly uncomplicated ideas together proves to be a little challenging.
There are only two crystal classes in the Triclinic System, the Pinacoidal Class and the Pedial Class. With a few more than 400 minerals that crystallize in the system, more than 300 crystallize in the Pinacoidal Class while only 50 are found in the Pedial Class. Approximately 70 minerals are considered to be Triclinic but have not been identified with either class.
The Triclinic Crystal System is unique in that it has either no symmetry at all, or that it has only a center of symmetry. Minerals crystallizing in this system have symmetry lower than each of the six other systems.
There are no rotational axes of symmetry and no mirror planes in the system. The Pinacoidal class has only a center of symmetry, and the Pedial class has no element of symmetry. Because of this, the minerals Of the pinacoidal class are bounded only by pinacoids (two parallel faces); and those of the pedial class show only pedions (single faces).
Unlike the other six crystal systems, the axes of the Triclinic System are not controlled by symmetry. There are no mirror planes and no axes of symmetry controlling crystallographic axes. As a result, different crystallographers have set the axes differently for the same mineral, which yields different axial ratios, axial angles, and Miller indices for the same crystal. Today, for professionals, x-ray analysis corrects the problem, but for collectors and amateur mineralogists examining a given crystal the problem persists.
The axes are of usually unequal length and intercept each other at unequal and usually oblique angles. However, there is nothing in the symmetry, or lack of it, that prevents one of the angles from being 90o. The axes are labelled a, b, and c. Generally, the most prominent zone is selected. (A zone is three or more faces with parallel edges surrounding a common axis, that is not necessarily a crystallographic axis.) The zone is oriented with the zone axis as the c-axis, in a vertical position, and one of the other axes, the a-axis, sloping downward toward the viewer and slightly left. The third axis, the b-axis, runs left to right. Axes are usually chosen so the a-axis is shorter than the b-axis. But this is not always so.
The angle between the b-axis and the c-axis is given the symbol, α (alpha). The angle between the a-axis and c-axis is β (beta). And the angle between the a-axis and the b-axis is γ (gamma). Perhaps the major characteristic to look for in identifying this system is the inclination of each of the axes to the others. Always keeping in mind that one of the angles may be 90o, and that any or all of the three may be very close to 90o. Look for the oblique angles.
Orienting a crystal that is in the Triclinic System presents some unique problems. Since there is very little, or no, symmetry, the direction of the axes is not at all obvious. Look for the large faces. If they were extended, do they seem to resemble a box? Keeping in mind that Triclinic crystals are made of only pinacoids or pedions, go ahead and think of it as a variation on a cube. A cube that is stretched in its proportions and probably out of shape. The similarity has some merit, as the faces despite the fact that they are pinacoids or pedions are somewhat likely to have the same Miller indices as the cube. Then, do the axes of the box, yield a clue to the axes of the crystal?
The same argument can be made for considering four inclined and converging faces that are similar as a leaning pyramid. Think of them as being derived from the top half of an octahedron (but remember that they are really the positive halves of probably two pinacoids, or four positive pedions). If the general form (see below) is present, it will most likely be a triangle and may be part of the "pyramid". And at least some of the other indices are likely the same as on the octahedron.
If you find that usually triangular face, it is the parametral plane from which all other faces are identified. Keeping the c-axis vertical, set that face at the top, front, right corner of the crystal.
If you have not found the parametral plane, the usual procedure is to look for the most prominent zone (a zone is 3 or more faces with parallel edges that surround and when extended enclose a zone axis). The zone most likely includes the largest faces. Turn the crystal so the zone axis is vertical. The zone axis is then the c-axis. Choose a prominent face in the zone and call it (010). Choose an uppermost face that intersects the c-axis and assign it as (001). The direction of the edge between (010) and (001) is the direction of the a-axis. Usually it is oriented to pitch downward towards you and slightly left.
There are two types of forms, general forms and special forms.
The general form intercepts all axes, each at a different axial unit distance. Thus the Miller index for each axis has a different value and may not be zero. It might be {123}, {325}. {413}. pr something similar.
Order in the Triclinic System:
In designating forms in the Triclinic System, most crystallographers use 1st through 4th order labels. 1st, 2nd, and 3rd order labels are applied to pinacoids that intercept two of the axes and are parallel to the third axis. 1st order denotes forms parallel to the a-axis. 2nd order is parallel to the b-axis. 3rd order is parallel to the c-axis. And 4th order intercepts all three axes, not being parallel to any of them.
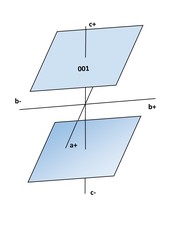
Triclinic Pinacoid: 2 faces, parallel to each other; General Form - {hkl} where h, k, and l may each have any value except 0. Special forms - {100}, (010) {00l}, {hk0}, {h0l}, or {0kl}, where h and l may be equal or different.
● Front, Side, Top Pinacoids: 2 faces, there are three pinacoids; each pair of faces intersects one axis and is parallel to the plane of the other two, respectively a, b, and c.
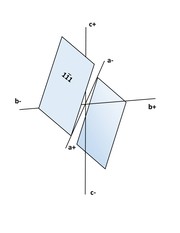
● 1st Order Pinacoids: 2 faces each, there are 2 of them; each pair of faces is parallel to the a-axis and intercepts the other two; if the upper face of the pinacoid intercepts the positive end of the b-axis, it is Positive, {0kl}; if the upper face of the pinacoid intercepts the negative end of the b_axis it is Negative, {0kl}.
● 2nd Order Pinacoid: 2 faces each, there are two of them, each pair of faces is parallel to the b-axis; in the same manner as for 1st Order, the intercepts on the a-axis determine which is Positive, {h0l} and which is Negative, {h0l}.
● 3rd Order Pinacoid: 2 faces each, there are two of them; they are parallel to the c-axis; {hk0} is Positive and {hk0} is Negative.
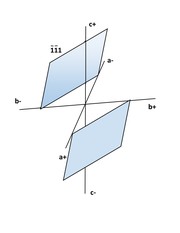
● 4th Order Pinacoid: 2 faces each, there are 4 of them; each face intercepts all three axes; Positive right, has its upper face {hkl} in the top right front octant; Positive left has its upper face {hkl}in the top left front octant, Negative right has the upper face {hkl) in the top right rear octant; and Negative left {hkl} has the upper face in the top left front octant.
Note: Position: All positions refer to the upper face of the pinacoid on the oriented crystal. Positive and Negative are determined by the axial sign of the end intercepted. And Left or Right is the side of the axial cross the face is on.
Note: For octant, think: octahedron.
Pedion: 1 face - There is not a similar face on the opposite side of the crystal. General form: {hkl} where h, k, l, may have any value, except 0. Special forms: {h00},{0k0},{h0l},{k0l}, h and l may be equal or different. Each form consists of a single face.
The symbols for the pinacoids and the pedions are the same. The pedion is considered to be derived as half of a pinacoid. In place of each possible pinacoid there are two possible pedions.
Minerals of the Triclinic System tend to be blocky, tabular, or lath-like. About 10% have acicular or radiated habits. In most cases, the crystals are visibly oblique in all three, or at least two, dimensions.
There are a few more than 300 minerals that crystallize in this class.
Hermann-Mauguin Symbol:
1 . . . . A center of symmetry.
Symmetry Elements:
C . . . . Center of symmetry. No axes of rotational symmetry, no mirror planes.
General Form:
Pinacoid: {hkl}, 2 faces
Special Forms:
Pinacoids: {h00} 2 faces
Pinacoids: {0k0} 2 faces
Pinacoids: {00l} 2 faces
Pinacoids: {hOl} 2 faces
Pinacoids: (0kl) 2 faces
Pinacoids: {hk0} 2 faces
Pinacoids: {hkl} 2 faces
Look For:
Look for the general shape of the crystal with axial angles that are not 90o in at least two directions, perhaps three directions. Look for faces similar to each other and parallel on opposite sides of the crystal. Every face should have a similar face parallel to it.
Problems:
Triclinic minerals often have axial angles within one or two degrees of 90o. And some have one of the angles = 90o.
Model: Albite
.
Symmetry:
...No axes of rotational symmetry
...No mirror planes of symmetry
...There is a Center of symmetry
..Orienting the Crystal:
...Set largest face w/ longest dimension to vertical.
...Turn crystal horizontally: vertical intersections of the edges are parallel (these faces are a zone).
...Assign the zone axis as the c-axis.
...Assign Miller indices (010) to the largest face; the b-axis emerges through that face.
...Find a large sloping face above (010): Assign Miller indices (001) to it. It is the plane of the a-axis and b-axis.
(001) slopes downward above the positive end of the a-axis: When looking at the face (010), if (001) slopes downward to your left the earlier assignment of (010) is correct. If not, it should be changed to (010) and the opposite face of the same pinacoid assigned (010).
..Axial Angles:
... α : Alpha is close to 95o (actual = 94o)
... β : Beta is close to 120o (actual = 116o)
... γ : Gamma is close to 90o (actual = 88o)
..Forms
...{010}: Side Pinacoid: intersects b-axis, parallel to the plane of a-axis and c-axis.
...{001): Basal Pinacoid: intersects c-axis, parallel to the plane of a-axis and b-axis.
...{110}: 3rd Order Pinacoid; parallel to c-axis, intersects both a+ axis and b+ axis.
...{110}: 3rd Order Pinacoid: parallel to c-axis, intersects the a+ axis and the b- axis.
...{110}: 3rd Order Pinacoid; parallel to c-axis, intersects both a- axis and b- axis.
...{111:} 4th Order Pinacoid: intersects all three axes.
...{111}: 4th Order Pinacoid: intersects all three axes.
Model: Rhodonite
Even though this crystal drawing is idealized, the analysis of its morphology is difficult.
.
1. Convince yourself that the crystal is triclinic. (Rotating the crystal, all major angles are oblique.)
2. Find 6 Large faces that are analogous to a cube. Are the faces pinacoids or pedions? (Pinacoids, opposite faces are similar and parallel)
3. Find the zone of the c-axis and orient the zone axis in a vertical position. (the c-axis zone faces all have parallel edges.)
4. Turn the crystal to view the top. Which of these faces is most likely is (001)? (The largest of the two.)
5. Can you see the direction of the a-axis. (Notice the parallelism of the faces at the ends of the top and the diagonal edge between the two largest faces on the top. That edge line is most likely the direction of the a-axis. The c-zone faces parallel to the a-axis would be (010) and (010) )
6. Find the direction of the b-axis. (The edge line between {001} and the small trapezoidal face might be the direction of the b-axis. The c-zone face below the trapezoid would be parallel to the b-axis and would be (100). The trapezoid is likely (101, parallel to the b-axis.)
.. Forms::
...Front Pinacoid: {100}: Parallel to the plane of the b-axis and c-axis.
...Basal Pinacoid: {001}: Parallel to the plane of the a-axis and b-axis.
...Side Pinacoid: {010}: Parallel to the plane of the a-axis and c-axis.
...1st Order Pinacoids: {012) (011): Parallel to the a-axis, intercepts the other two.
...2nd Order Pinacoids: {101} {101}{102) {201}: Parallel to the a-axis, intercepts the other two.
...3rd Order Pinacoid: {110}: Parallel to the c-axis, intercepts the other two.
Representative Minerals: Click the name to access the Mineral Page
Albite, Amblygonite, Babingtonite, Chalcanthite, Kyanite, Microcline, Rhodonite
There are approximately 70 minerals in this class, all of them rare.
Hermann-Mauguin Symbol:
1 . . . .No symmetry elements
Symmetry:
None
Look For:
Look for apparent axial angles not equal to 90o in at least two directions. Then search for pedions, single faces with no matching parallel face on the opposite side or end.
Problems:
Not only are the minerals in this class rare, but good crystals are even more uncommon, and they are most often microscopic. Analcime, a fairly common mineral, is classified in the pedial class but may be cubic, tetragonal, orthorhombic, or monoclinic depending upon slight changes in structural ordering.
Representative Minerals:
Analcime, Welshite
Crystallography: The Triclinic System
Crystallography: The Monoclinic System
Crystallography: The Orthohombic System
Crystallography: The Trigonal System
Crystallography: The Hexagonal System
Crystallography: The Tetragonal System
Crystallography: The Isometric System
Mason, Brian and Berry, L.G. (1968) Elements of Mineralogy. W. H. Freeman and Company, San Francisco.
Dana,Edward Salisbury; Foord, William E. (editor); A Textbook of Mineralogy. John Wiley & Sons, Inc., New York
Sinkankas, John: Mineralogy: A First Course. A great book with which to start.
Peck, Donald B. (2007) Mineral Identification: A Practical Guide for the Amateur Mineralogist. Mineralogical Record, Tucson, Arizona.
A.E.H Tutton,Crystallography and Practical Crystal Measurement Volume 1 Form and Structure; 2018. An incredibly thorough text. Not for the beginner.
Klein, Cornelis & Hurlbut, Cornelius S., Jr.: Manual of Mineralogy after J. D. Dana;20th Edition
http://www.minsocam.org/ammin/AM20/AM20_838.pdf: Rogers, Austin F. (1935) A historical discussion of the names of crystal forms.
https://en.wikipedia.org/wiki/Monoclinic_crystal_system , Short explanation of lattices, space groups, hemimorphic & enantiomorphic structure.
In some respects, the Triclinic Crystal System is the simplest of the seven systems. In other ways it is the most difficult to comprehend. There is little or no symmetry. And there are only two simple crystallographic forms to consider. Putting these two seemingly uncomplicated ideas together proves to be a little challenging.
There are only two crystal classes in the Triclinic System, the Pinacoidal Class and the Pedial Class. With a few more than 400 minerals that crystallize in the system, more than 300 crystallize in the Pinacoidal Class while only 50 are found in the Pedial Class. Approximately 70 minerals are considered to be Triclinic but have not been identified with either class.
You may find it helpful to review the following articles before attempting this one:
Determining Symmetry of Crystals: An Introduction
Miller Indices
Hermann-Mauguin Symmetry Symbols
Determining Symmetry of Crystals: An Introduction
Miller Indices
Hermann-Mauguin Symmetry Symbols
The Unique Symmetry Element of the Triclinic Crystal System
The Triclinic Crystal System is unique in that it has either no symmetry at all, or that it has only a center of symmetry. Minerals crystallizing in this system have symmetry lower than each of the six other systems.
There are no rotational axes of symmetry and no mirror planes in the system. The Pinacoidal class has only a center of symmetry, and the Pedial class has no element of symmetry. Because of this, the minerals Of the pinacoidal class are bounded only by pinacoids (two parallel faces); and those of the pedial class show only pedions (single faces).
The Crystallographic Axes
Unlike the other six crystal systems, the axes of the Triclinic System are not controlled by symmetry. There are no mirror planes and no axes of symmetry controlling crystallographic axes. As a result, different crystallographers have set the axes differently for the same mineral, which yields different axial ratios, axial angles, and Miller indices for the same crystal. Today, for professionals, x-ray analysis corrects the problem, but for collectors and amateur mineralogists examining a given crystal the problem persists.
The axes are of usually unequal length and intercept each other at unequal and usually oblique angles. However, there is nothing in the symmetry, or lack of it, that prevents one of the angles from being 90o. The axes are labelled a, b, and c. Generally, the most prominent zone is selected. (A zone is three or more faces with parallel edges surrounding a common axis, that is not necessarily a crystallographic axis.) The zone is oriented with the zone axis as the c-axis, in a vertical position, and one of the other axes, the a-axis, sloping downward toward the viewer and slightly left. The third axis, the b-axis, runs left to right. Axes are usually chosen so the a-axis is shorter than the b-axis. But this is not always so.
The angle between the b-axis and the c-axis is given the symbol, α (alpha). The angle between the a-axis and c-axis is β (beta). And the angle between the a-axis and the b-axis is γ (gamma). Perhaps the major characteristic to look for in identifying this system is the inclination of each of the axes to the others. Always keeping in mind that one of the angles may be 90o, and that any or all of the three may be very close to 90o. Look for the oblique angles.
Orienting A Crystal:
Orienting a crystal that is in the Triclinic System presents some unique problems. Since there is very little, or no, symmetry, the direction of the axes is not at all obvious. Look for the large faces. If they were extended, do they seem to resemble a box? Keeping in mind that Triclinic crystals are made of only pinacoids or pedions, go ahead and think of it as a variation on a cube. A cube that is stretched in its proportions and probably out of shape. The similarity has some merit, as the faces despite the fact that they are pinacoids or pedions are somewhat likely to have the same Miller indices as the cube. Then, do the axes of the box, yield a clue to the axes of the crystal?
The same argument can be made for considering four inclined and converging faces that are similar as a leaning pyramid. Think of them as being derived from the top half of an octahedron (but remember that they are really the positive halves of probably two pinacoids, or four positive pedions). If the general form (see below) is present, it will most likely be a triangle and may be part of the "pyramid". And at least some of the other indices are likely the same as on the octahedron.
If you find that usually triangular face, it is the parametral plane from which all other faces are identified. Keeping the c-axis vertical, set that face at the top, front, right corner of the crystal.
If you have not found the parametral plane, the usual procedure is to look for the most prominent zone (a zone is 3 or more faces with parallel edges that surround and when extended enclose a zone axis). The zone most likely includes the largest faces. Turn the crystal so the zone axis is vertical. The zone axis is then the c-axis. Choose a prominent face in the zone and call it (010). Choose an uppermost face that intersects the c-axis and assign it as (001). The direction of the edge between (010) and (001) is the direction of the a-axis. Usually it is oriented to pitch downward towards you and slightly left.
General and Special Forms.
There are two types of forms, general forms and special forms.
Any form which is not a general form is a special form. Most often, the general form is the form for which the crystal class is named. A general form has the maximum number of faces of any form in its crystal class. Special forms are not unique to a particular class but may appear in several classes.
The general form intercepts all axes, each at a different axial unit distance. Thus the Miller index for each axis has a different value and may not be zero. It might be {123}, {325}. {413}. pr something similar.
Forms in the | ||||||||||||||||||||||||||||||
|
Order in the Triclinic System:
In designating forms in the Triclinic System, most crystallographers use 1st through 4th order labels. 1st, 2nd, and 3rd order labels are applied to pinacoids that intercept two of the axes and are parallel to the third axis. 1st order denotes forms parallel to the a-axis. 2nd order is parallel to the b-axis. 3rd order is parallel to the c-axis. And 4th order intercepts all three axes, not being parallel to any of them.
Triclinic Pinacoid: 2 faces, parallel to each other; General Form - {hkl} where h, k, and l may each have any value except 0. Special forms - {100}, (010) {00l}, {hk0}, {h0l}, or {0kl}, where h and l may be equal or different.
● Front, Side, Top Pinacoids: 2 faces, there are three pinacoids; each pair of faces intersects one axis and is parallel to the plane of the other two, respectively a, b, and c.
● 1st Order Pinacoids: 2 faces each, there are 2 of them; each pair of faces is parallel to the a-axis and intercepts the other two; if the upper face of the pinacoid intercepts the positive end of the b-axis, it is Positive, {0kl}; if the upper face of the pinacoid intercepts the negative end of the b_axis it is Negative, {0kl}.
● 2nd Order Pinacoid: 2 faces each, there are two of them, each pair of faces is parallel to the b-axis; in the same manner as for 1st Order, the intercepts on the a-axis determine which is Positive, {h0l} and which is Negative, {h0l}.
● 3rd Order Pinacoid: 2 faces each, there are two of them; they are parallel to the c-axis; {hk0} is Positive and {hk0} is Negative.
● 4th Order Pinacoid: 2 faces each, there are 4 of them; each face intercepts all three axes; Positive right, has its upper face {hkl} in the top right front octant; Positive left has its upper face {hkl}in the top left front octant, Negative right has the upper face {hkl) in the top right rear octant; and Negative left {hkl} has the upper face in the top left front octant.
Note: Position: All positions refer to the upper face of the pinacoid on the oriented crystal. Positive and Negative are determined by the axial sign of the end intercepted. And Left or Right is the side of the axial cross the face is on.
Note: For octant, think: octahedron.
Pedion: 1 face - There is not a similar face on the opposite side of the crystal. General form: {hkl} where h, k, l, may have any value, except 0. Special forms: {h00},{0k0},{h0l},{k0l}, h and l may be equal or different. Each form consists of a single face.
The symbols for the pinacoids and the pedions are the same. The pedion is considered to be derived as half of a pinacoid. In place of each possible pinacoid there are two possible pedions.
General Morphology:
Minerals of the Triclinic System tend to be blocky, tabular, or lath-like. About 10% have acicular or radiated habits. In most cases, the crystals are visibly oblique in all three, or at least two, dimensions.
Triclinic Crystal Classes:
Pinacoidal Class:
There are a few more than 300 minerals that crystallize in this class.
Hermann-Mauguin Symbol:
1 . . . . A center of symmetry.
Symmetry Elements:
C . . . . Center of symmetry. No axes of rotational symmetry, no mirror planes.
General Form:
Pinacoid: {hkl}, 2 faces
Special Forms:
Pinacoids: {h00} 2 faces
Pinacoids: {0k0} 2 faces
Pinacoids: {00l} 2 faces
Pinacoids: {hOl} 2 faces
Pinacoids: (0kl) 2 faces
Pinacoids: {hk0} 2 faces
Pinacoids: {hkl} 2 faces
Look For:
Look for the general shape of the crystal with axial angles that are not 90o in at least two directions, perhaps three directions. Look for faces similar to each other and parallel on opposite sides of the crystal. Every face should have a similar face parallel to it.
Problems:
Triclinic minerals often have axial angles within one or two degrees of 90o. And some have one of the angles = 90o.
Model: Albite
Symmetry:
...No axes of rotational symmetry
...No mirror planes of symmetry
...There is a Center of symmetry
..Orienting the Crystal:
...Set largest face w/ longest dimension to vertical.
...Turn crystal horizontally: vertical intersections of the edges are parallel (these faces are a zone).
...Assign the zone axis as the c-axis.
...Assign Miller indices (010) to the largest face; the b-axis emerges through that face.
...Find a large sloping face above (010): Assign Miller indices (001) to it. It is the plane of the a-axis and b-axis.
(001) slopes downward above the positive end of the a-axis: When looking at the face (010), if (001) slopes downward to your left the earlier assignment of (010) is correct. If not, it should be changed to (010) and the opposite face of the same pinacoid assigned (010).
..Axial Angles:
... α : Alpha is close to 95o (actual = 94o)
... β : Beta is close to 120o (actual = 116o)
... γ : Gamma is close to 90o (actual = 88o)
..Forms
...{010}: Side Pinacoid: intersects b-axis, parallel to the plane of a-axis and c-axis.
...{001): Basal Pinacoid: intersects c-axis, parallel to the plane of a-axis and b-axis.
...{110}: 3rd Order Pinacoid; parallel to c-axis, intersects both a+ axis and b+ axis.
...{110}: 3rd Order Pinacoid: parallel to c-axis, intersects the a+ axis and the b- axis.
...{110}: 3rd Order Pinacoid; parallel to c-axis, intersects both a- axis and b- axis.
...{111:} 4th Order Pinacoid: intersects all three axes.
...{111}: 4th Order Pinacoid: intersects all three axes.
Model: Rhodonite
Even though this crystal drawing is idealized, the analysis of its morphology is difficult.
1. Convince yourself that the crystal is triclinic. (Rotating the crystal, all major angles are oblique.)
2. Find 6 Large faces that are analogous to a cube. Are the faces pinacoids or pedions? (Pinacoids, opposite faces are similar and parallel)
3. Find the zone of the c-axis and orient the zone axis in a vertical position. (the c-axis zone faces all have parallel edges.)
4. Turn the crystal to view the top. Which of these faces is most likely is (001)? (The largest of the two.)
5. Can you see the direction of the a-axis. (Notice the parallelism of the faces at the ends of the top and the diagonal edge between the two largest faces on the top. That edge line is most likely the direction of the a-axis. The c-zone faces parallel to the a-axis would be (010) and (010) )
6. Find the direction of the b-axis. (The edge line between {001} and the small trapezoidal face might be the direction of the b-axis. The c-zone face below the trapezoid would be parallel to the b-axis and would be (100). The trapezoid is likely (101, parallel to the b-axis.)
.. Forms::
...Front Pinacoid: {100}: Parallel to the plane of the b-axis and c-axis.
...Basal Pinacoid: {001}: Parallel to the plane of the a-axis and b-axis.
...Side Pinacoid: {010}: Parallel to the plane of the a-axis and c-axis.
...1st Order Pinacoids: {012) (011): Parallel to the a-axis, intercepts the other two.
...2nd Order Pinacoids: {101} {101}{102) {201}: Parallel to the a-axis, intercepts the other two.
...3rd Order Pinacoid: {110}: Parallel to the c-axis, intercepts the other two.
Representative Minerals: Click the name to access the Mineral Page
Albite, Amblygonite, Babingtonite, Chalcanthite, Kyanite, Microcline, Rhodonite
Pedial Class:
There are approximately 70 minerals in this class, all of them rare.
Hermann-Mauguin Symbol:
1 . . . .No symmetry elements
Symmetry:
None
Look For:
Look for apparent axial angles not equal to 90o in at least two directions. Then search for pedions, single faces with no matching parallel face on the opposite side or end.
Problems:
Not only are the minerals in this class rare, but good crystals are even more uncommon, and they are most often microscopic. Analcime, a fairly common mineral, is classified in the pedial class but may be cubic, tetragonal, orthorhombic, or monoclinic depending upon slight changes in structural ordering.
Representative Minerals:
Analcime, Welshite
Links to the Crystallography of Each of the Systems.
Crystallography: The Triclinic System
Crystallography: The Monoclinic System
Crystallography: The Orthohombic System
Crystallography: The Trigonal System
Crystallography: The Hexagonal System
Crystallography: The Tetragonal System
Crystallography: The Isometric System
References:
Mason, Brian and Berry, L.G. (1968) Elements of Mineralogy. W. H. Freeman and Company, San Francisco.
Dana,Edward Salisbury; Foord, William E. (editor); A Textbook of Mineralogy. John Wiley & Sons, Inc., New York
Sinkankas, John: Mineralogy: A First Course. A great book with which to start.
Peck, Donald B. (2007) Mineral Identification: A Practical Guide for the Amateur Mineralogist. Mineralogical Record, Tucson, Arizona.
A.E.H Tutton,Crystallography and Practical Crystal Measurement Volume 1 Form and Structure; 2018. An incredibly thorough text. Not for the beginner.
Klein, Cornelis & Hurlbut, Cornelius S., Jr.: Manual of Mineralogy after J. D. Dana;20th Edition
http://www.minsocam.org/ammin/AM20/AM20_838.pdf: Rogers, Austin F. (1935) A historical discussion of the names of crystal forms.
https://en.wikipedia.org/wiki/Monoclinic_crystal_system , Short explanation of lattices, space groups, hemimorphic & enantiomorphic structure.
Acknowledgements:
Photo Credits: Chabazite-Ca: Rob Lavinsky; Kyanite: Rob Lavinsky & Irocks; Microcline: Leon Huppericks; Analcime: John H. Betts; Epistilbite: Volker Betz.Article has been viewed at least 25193 times.